这是3月25日我在TM组机器学习讨论会上的分享。
Content
- 贝叶斯决策论
- 朴素贝叶斯分类器
- 半朴素贝叶斯分类器
- 贝叶斯网络
1. 贝叶斯决策论
贝叶斯决策论是一种基于概率的决策理论。当所有相关的概率都已知的理想情况下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
Example
哈工大与哈师大的同学举办大型联♂谊♀会,两个学校分别有500人参与。在联谊会上随机找到一个同学,请猜测他是那个学校的学生?
如果我们一点额外信息都不知道的话,只能随机猜测给出答案。如果我们能够提前知道一点点信息的话,就能够更大程度地猜中正确答案。比如,性别信息:

如此的话,假若这个同学是男生,我们肯定会猜测他是哈工大的学生。而从贝叶斯决策论的角度来看,我们需要比较以下两个概率大小:
- P(工大学生=是 | 性别 = X)
- P(师大学生=是 | 性别 = X)
上述两个概率被称作后验概率。后验概率往往难以直接获得,我们需要采用一定的手段进行计算。一些算法采用直接对后验概率进行建模的方法,例如SVM、决策树等,这些模型称为判别式模型。而先对联合概率进行建模、进而计算后验概率的模型,称为生成式模型:
\(P(c|\boldsymbol{x})=\frac{P(\boldsymbol{x}, c)}{P(\boldsymbol{x})}=\frac{P(c)P(\boldsymbol{x}|c)}{P(\boldsymbol{x})}\)
由此可以计算得到,P(工大学生=是 | 性别 = 男)为4/5,P(师大学生=是 | 性别 = 男)为1/5.
在上面的例子中,我们直接使用了后验概率对类别进行估计。实际问题中,如果将某一类估计错误的代价比较大的话,可以选择在后验概率前乘以一个系数,变为期望损失。分类也从最小化分类错误率变为最小化期望损失。
在上面的式子中,\(P(c)\)代表的是类先验概率。在样本足够大的情况下,直接使用频率即可作为这一概率;\(P(\boldsymbol{x}|c)\)叫做类条件概率,它跟属性x的联合概率有关。上面的例子中,x只有一维,而在实际问题中,往往会选择很多个Feature。此时他们的联合概率就变得难以计算,因此我们需要一些手段对它们进行估计。
2. 朴素贝叶斯分类器
朴素贝叶斯分类器假设所有的属性之间独立同分布,使得计算他们的联合概率变得非常简单。此时后验概率公式变为:
\[P(c|\boldsymbol{x})=\frac{P(c)}{P(\boldsymbol{x})}\prod_{i=1}^{d}P(x_i|c)\]
对于取值为离散的属性来说,通过最大似然估计后的结果为\(P(x_i|c)=\frac{|D_{c,xi}|}{|D_c|}\),即样本中第i个属性取值为xi的样本个数在当前类别中的的频率。而对于连续值来说,我们需要假设它服从某个特定的分布。假设属性\(x_i\)的条件概率服从正态分布的话,则根据最大似然估计结果,我们可以做出如下估计:
\[p(x_i|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,i}}exp(-\frac{(x_i-\mu_{c,i})^2}{2\sigma^2_{c,i}})\]
其中的\(\mu\)和\(\sigma\)分别是样本中属于C类的第i个属性的均值和标准差。
然而,如果某一个属性的取值在某一类样本中没有出现过的话, 按照上面的\(P(x_i|c)=\frac{|D_{c,xi}|}{|D_c|}\)公式进行计算后,由于\(|D_{c,xi}|=0\),其条件概率为0,而在连乘后将导致整个后验概率为0。在这种情况下,这一个属性就决定了整个分类结果,这是不合理的。
导致出现这种情况的原因是:由于样本容量有限,这些属性值没有在样本中被观测到,而并不是其出现的概率为0。为了解决这个问题,我们可以使用一些平滑策略,例如拉普拉斯修正:
\[P(c)=\frac{|D_c|+1}{|D|+N}\] \[P(x_i|c)=\frac{|D_{c,xi}|+1}{|D_c|+N_i}\]
即在分子+1,分母加上当前类别或属性可能的取值个数。
2. 半朴素贝叶斯分类器
朴素贝叶斯分类器假设了每个属性之间独立同分布,这一假设较强,实际问题中属性之间往往存在一定的依赖关系。
半朴素分类器将这一条件适当放宽,它假设每一个属性最多只依赖于一个其他属性,称作它的父属性。如何从样本中估计出每一个元素的父属性,是半朴素贝叶斯分类器要解决的重点问题。对每个元素的父属性的估计称作独依赖估计(ODE),不同的独依赖估计方法将会产生不同的半朴素贝叶斯分类器。公式可表示为:
\[P(c|x)\propto P(c)\prod_{i=1}^{d}P(x_i|c,pa_i)\]
其中\(pa_i\)表示父属性。
超父独依赖估计(SP-ODE)
在超父独依赖估计的模型中,假设了所有其他属性均依赖于同一个父属性,这一个属性就被称作“超父”(Super Parent)。通过交叉验证等手段,可以选择出出最优的那一个“超父”。
树增强朴素贝叶斯(Tree Augment Naive Bayes, TAN) TAN通过计算每两个属性之间的条件互信息来确定依赖关系。步骤如下:
- 计算每两个属性之间的条件互信息
- 以属性为节点构建完全图,边的权重为条件互信息
- 构建完全图的最大生成树,从中选择一个节点为根节点,把所有的边改为有向边,方向为由根节点向外的方向。
TAN只保留了强相关属性之间的依赖性。
Average ODE
AODE采取的方案是去掉出现次数过少的属性,将剩余的属性集成起来,使用公式表达如下:
\[P(c|x)\propto \sum_{i=1;|D_{xi}|\geq m}^d P(c,x_i)\prod_{j=1}^{d}P(x_j|c,x_i)\]
贝叶斯网
贝叶斯网进一步减弱了关系之间的刻画方式,不再要求每个属性只依赖于一个父属性。它采用了有向无环图对依赖关系进行描述,同时在每一组依赖关系上还需要一张条件概率表来表示属性的联合概率分布:
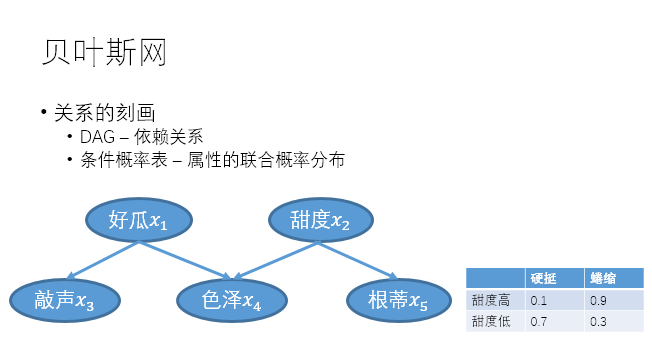
\[B=\langle G,\Theta \rangle\]
在上述的贝叶斯网中,x1~x5的联合概率可表示为\(P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3|x_1)P(x_4|x_1,x_2)P(x_5|x_2)\)
在一个贝叶斯网中,常见的结构如下:
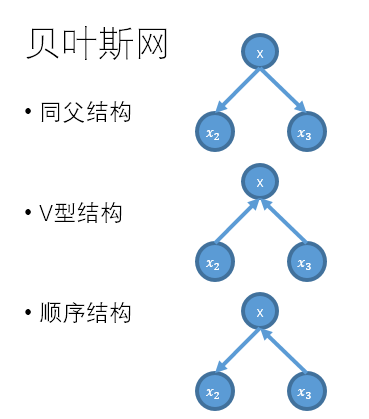
对于同父结构,给定x,x2和x3相互独立; 对于顺序结构,给定x,x2和x3相互独立; 对于V型结构,给定x,x2和x3不独立;而不给定x,x2和x3相互独立。
为了更简便地分析网中变量之间的独立性,我们可以使用道德图。将贝叶斯网的有向图转为道德图的步骤如下:
- 找出有向图中所有的V型结构
- 将父节点之间添加一条无香边
- 所有有向边改为无向边
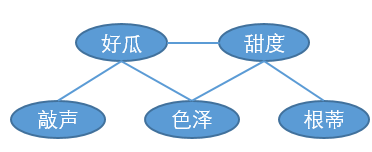
给定一些属性值后,如何判断其他属性之间的独立性呢?只需要在道德图中将给定的属性节点去掉,如果两个属性之间不再连通,则它们相互独立。
学习
如果依赖关系已知的情况下,学习一个贝叶斯网就是一个计数的过程。然而实际问题中往往这种关系未知,我们需要学习一个。构建贝叶斯网的常用方法是引入一个评分函数,它的值代表了当前的网与样本的拟合程度。一种基于信息论准则的评分准则是“最小描述长度”准则,我们使用字符串来编码一个贝叶斯网,每个网对应一个字符串。字符串长度越短,代表贝叶斯网最优。因此学习目标就是找到一个能以最短编码长度描述训练数据的模型。
最小描述长度准则
综合编码长度=DAG编码长度+条件概率表编码长度。给定训练集𝐷={𝑥1,𝑥2,…,𝑥𝑚},贝叶斯网B的评分函数为
\[s(B|D)=f(\theta)|B|+LL(B|D)\]
第一项是网的结构的编码,其中对|B|代表贝叶斯网的参数个数,\(f(\theta)\)代表了描述每个参数需要的字节数。
第二项是对数似然函数\(LL(B|D)=\sum_{i=1}^{m}logP(x_i)\),代表了编码条件概率表需要的字节长度。
当网结构固定时,第一项为常数,第二项能够从训练数据中计算得到,因此整个优化过程主要集中在如何选择贝叶斯网的依赖结构。精确地搜索所有可能的网络结构是一个NP难的问题,常用的近似方法包括贪心得到局部最优解、限定网络结构为树状结构等。
推断
推断表示的是通过一些属性的观测值来推断其他属性的值。其精确计算也是NP难的问题。通常采用吉布斯采样进行近似,吉布斯采样通过随机初值、“随机漫步”的方式得到一组合理的近似解。在将未知节点随机赋予初值后,依次更新所有未知节点,更新的依据就是其他节点的值。当所有的未知节点更新完一次后,即完成了一轮迭代。
吉布斯采样的每一次迭代都只与上一次的状态有关,因此它其实是在解空间中走出了一个马尔科夫链。马尔科夫链在经历足够多的迭代次数后将趋于收敛,对于这里的吉布斯采样来说它将收敛于一组近似解。
EM算法
前面所提到的几个贝叶斯分类器都要求训练数据的完整性,即不能存在未观测的属性。然而在实际试验中可能会出现这样的问题,例如西瓜的根部掉落,从而无法得知它根部的属性。这种未观测变量被叫做隐变量。存在隐变量时,对数似然无法直接计算:\(LL(\Theta|X,Z)=lnP(X,Z|\Theta)\),其中Z代表隐变量。不过,我们可以计算它的边际似然:
\[LL(\Theta|X)=lnP(X|\Theta)=ln\sum_ZP(X,Z|\Theta)\]
EM算法分为两步:
- E步:根据上一次计算得到的\(\Theta\),计算Z的期望。对于首次计算,使用初值\(\Theta^0\)
- M步:根据Z的期望计算\(\Theta\)的最大似然估计
Reference
周志华.《机器学习》. 清华大学出版社, 2016.
